280. Вершина
В
ориентированном графе найти вершины, недостижимые из заданных вершин.
Вход. Первая строка содержит количество
вершин в графе n (1 £ n
£ 100). Каждая следующая строка содержит
последовательность чисел i, a1, …, ak,
0 (оканчивающуюся нулем), описывающую ребра i ® a1, i ® a2, ... i ® ak. Описание ребер завершается строкой из
единственного нуля. Следующая строка содержит количество исследуемых вершин
вместе с их номерами. Далее идет описание следующего графа. Описание графов
заканчивается строкой из одного нуля.
Выход. Для
каждой исследуемой вершины в отдельной строке вывести количество недостижимых
из нее вершин, а также номера этих вершин.
|
Пример входа |
Пример выхода |
|
3 1 2 0 2 2 0 3 1 2 0 0 2 1 2 0 |
2 1 32 1 3 |
РЕШЕНИЕ
графы, алгоритм
Флойда - Уоршела
Анализ алгоритма
Построим матрицу смежности графа c. Запустим
алгоритм Флойда – Уоршела поиска всех путей в графе. Для вершины i
недостижимыми будут те вершины j, для которых будет c[i][j]
= ¥ после выполнения алгоритма Флойда – Уоршела. Сложность
алгоритма O(n3).
Пример
Рассмотрим
заданный в условии пример, изобразим граф:
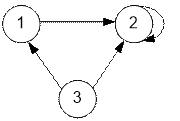
В примере
исследуются две вершины: первая и вторая. Как из первой, так и со второй
вершины невозможно попасть в первую и третью вершину.
Реализация
алгоритма
Входной граф
храним в матрице смежности c размера MAX = 101.
#define MAX 101
int c[MAX][MAX];
Реализация
алгоритма Флойда – Уоршела:
void floyd(void)
{
int i, j, k;
for(k = 1; k <= n; k++)
for(i = 1; i <= n; i++)
for(j = 1; j <= n; j++)
if (c[i][k] + c[k][j] < c[i][j])
c[i][j] = c[i][k] + c[k][j];
}
Основной цикл
программы. Читаем данные графа и строим матрицу смежности c. Изначально
полагаем все ребра равными бесконечности (в качестве бесконечности выберем шестнадцатеричное
значение 3F3F3F3F). Поскольку вершины графа по условию задачи нумеруются с
единицы, то нулевая строка и столбец матрицы c задействованы не будут.
while(scanf("%d",&n), n > 0)
{
memset(c,0x3F,sizeof(c));
while(scanf("%d",&a) ,a)
while(scanf("%d",
&b), b) c[a][b] = 1;
Запускаем на
матрице смежности c алгоритм Флойда – Уоршела.
floyd();
Читаем
количество исследуемых вершин i для заданного графа, и для каждой исследуемой
вершины a подсчитываем количество вершин b, недостижимых из a
(для которых c[a][b] = ¥).
scanf("%d",&i);
while(i--)
{
scanf("%d",&a);
Подсчет
количества вершин, недостижимых из a.
for(count = 0, b = 1; b <= n; b++)
if (c[a][b] == 0x3F3F3F3F) count++;
Печать
количества недостижимых вершин из a и самих вершин
в порядке возрастания номеров.
printf("%d",count);
for(b = 1; b <= n; b++)
if (c[a][b]
== 0x3F3F3F3F) printf(" %d",b);
printf("\n");
}
}